Trigonometri #8

8.       Rumus-rumus umum bagi sebarang sudut

$latex \color{blue}\large\bf\alpha +k.360^\circ $

$latex \color{blue}sin(\alpha +k.360^\circ )=sin\alpha $

$latex \color{blue}cos(\alpha +k.360^\circ )=cos\alpha $

$latex \color{blue}tan(\alpha +k.360^\circ )=tan\alpha $

dengan $latex k$ bilangan bulat.

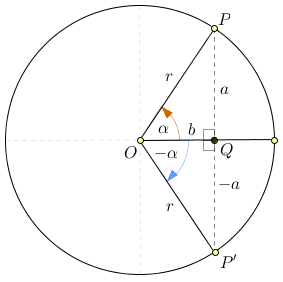
Sudut negatif

$latex sin(-\alpha )=\frac{-a}{r}=-sin\alpha $

$latex cos(-\alpha )=\frac{b}{r}=cos\alpha $

$latex tan(-\alpha )=\frac{-a}{b}=-tan\alpha $

$latex \color{blue}\large\bf\alpha +k.180^\circ $

$latex \color{Orchid}sin(\alpha \pm k.180^\circ )=-sin\alpha $

$latex \color{Orchid}cos(\pm \alpha \pm k.180^\circ)=-cos\alpha $

$latex \color{Orchid}tan(\alpha \pm k.180^\circ)=tan\alpha $

sehingga diperoleh bentuk umum:

$latex \color{blue}sin(\alpha +k.180^\circ )=(-1)^{k}\ sin\alpha $

$latex \color{blue}cos(\pm \alpha +k.180^\circ )=(-1)^{k}\ cos\alpha $

$latex \color{blue}tan(\alpha +k.180^\circ )=tan\alpha $

dengan $latex k$ bilangan bulat.

Adjie Gumarang Pujakelana, 2013


-->