Irisan Kerucut #1

Kerucut

Misalkan garis$latex g$dan garis$latex s$berpotongan di titik$latex P$dan membentuk sudut sebesar$latex \alpha$.

Kerucut adalah bangun ruang yang terjadi jika$latex g$diputar pada$latex P$mengelilingi$latex s$dengan$latex \alpha$tetap.
Kerucut yang terjadi adalah kerucut tegak berdaun ganda.


$latex P$disebut titik puncak kerucut.
$latex g_{1},\ g_{2},\ g_{3},\ ...$disebut garis-garis pelukis (generator).
$latex s$disebutsumbu kerucut.
$latex \alpha$disebutsetengah sudut puncak.
$latex \{g_{1},\ g_{2},\ g_{3},\ ...\}$disebut selimut kerucut.






Irisan Kerucut

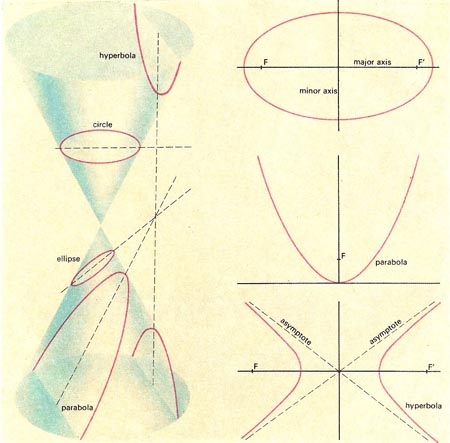
Irisan kerucut adalah irisan yang terjadi jika kerucut itu diiris oleh suatu bidang datar, tetapi tidak melalui titik puncaknya.

Bentuk irisan kerucut dapay diselidiki berdasarkan:

a. Kedudukan bidang pengiris
     (1) Jika mengiris salah satu selimut kerucut dan
          i.  tegak lurus terhadap sumbu kerucut, maka irisannya 
              berbentuk lingkaran.
          ii. tidak tegak lurus terhadap sumbu kerucut, maka irisannya 
              berbentuk elips.
     (2) Jika sejajar dengan salah satu garis pelukis, maka irisannya 
           berbentuk parabola.
     (3) Jika mengiris kedua selimut kerucut, maka irisannya berbentuk 
          hiperbola.

b. Sudut antara bidang pengiris dan sumbu kerucut
    Misalkan$latex \beta$adalah besar sudut antara bidang pengiris dan sumbu 
    kerucut.
    (1) Jika$latex \beta =90^\circ$maka irisannya berbentuk lingkaran.
    (2) Jika$latex \alpha =\beta$maka irisannya berbentuk parabola.
    (3) Jika$latex \alpha <\beta$maka irisannya berbentuk elips.
                                                                                                              (4) Jika$latex \alpha >\beta$maka irisannya berbentuk hiperbola.

c. Eksentrisitas (khusus untuk parabola/elips/hiperbola)

Definisi: Irisan kerucut (parabola/elips/hiperbola) adalah tempat kedudukan titik-titik yang 
              perbandingan jaraknya ke titik tertentu dan ke garis tertentu bernilai tetap.

Titik tertentu itu disebut titik fokus (F).
Garis tertentu itu disebut garis arah (direktriks).
Perbandingan tertentu itu disebut eksentrisitas (e) dengan$latex e=\frac{PF}{PQ}$.
(1) Jika $latex e=1$maka irisannya berbentuk parabola.
(2) Jika $latex 0<e<1$maka irisannya berbentuk elips.
(3) Jika $latex e>1$maka irisannya berbentuk hiperbola.